Segment Tree in java

If you want to practice data structure and algorithm programs, you can go through Java coding interview questions.

In this post, we will see about Segment Tree in java.

Problem

Consider an Array of Integers,
int[] arr = {a1, a2, a3, a4, a5,….., an};

Given two types of queries,
(i) In the first type of query, given two integers, L & R, Output the sum of the elements in the
given range.
(ii) In the second type of query, given an Index and a value, update the value in array at the
given index to the given value.

Input format:
First line will contain an integer n, that is, the length of the given array.
Next line contains N space separated integers which are the elements of the array.
next line will contain the number of queries.
Next q lines will contain 2 space separated integers, if the first integer is ‘1’ then it will be a range sum query, if the first integer is ‘2’ then it will be an update query.

Here
1 2 4
1 represents range sum query, so we need to find sum of elements from index to 2 to 4.
so answer is 6 (4 + -3 + 5)

2 3 3
2 represents update query, so we will update index 3 with value 3 in the array, so array will become
2 6 4 3 5 -1 6 10

1 2 4
Again same query as before but since value at index 3 is updated, we will get result as 12 (4 + 3 + 5)

Solution

Approach – I:

• For the first type of query, when the sum of the given range is asked, we run a loop from L to R and add the every every element in the range to a variable and output the variable to give the sum of the given range.
• For second type of query, we update the value at the given index in the query.
  The complexity for the range query operation is O(n) and for update operation it is O(1) as we directly reach to the given index and update the value which takes constant time.
• Therefore, overall worst time complexity of this approach is : O(n) + O(1)
                                                                                                                                 : O(n)

Approach – II:

Instead of looping in whole array every time to find a range sum, we can create a prefix sum array in O(n) time before we solve any query. This prefix sum array contains the sum of the array starting from 0th index to i th index in the given array. This boils down the time complexity for range sum query to O(1) as the sum of range [L,R] can be found by,

• rangesum = prefixsum[R] – prefixsum[L-1]       {where L > 0}
  rangesum = prefixsum[R]                                        {where L = 0}

Now for update query, whenever an element in the given array is changed, the prefix sum of all the indices in range [i, arr.length()] is effected. Now the worst time complexity for updation becomes O(n).
The worst time complexity for this approach will again be : O(1) + O(n) = O(n)

Efficient Approach :

For solving the range queries and updates which can be point or range, we use Segment tree which is basically a full binary tree that is for every parent there will be either 2 or no children, which is used to solve range queries and updations efficiently in O(logN). These range queries can be of any type such as, range sum, range min, range max, range GCD, etc. It also handles the point updation and also the range update which we will see in the later part of the article.
In this article we will discuss the calculation of Range Sum Query and point updates using Segment tree in O(log n) time complexity.

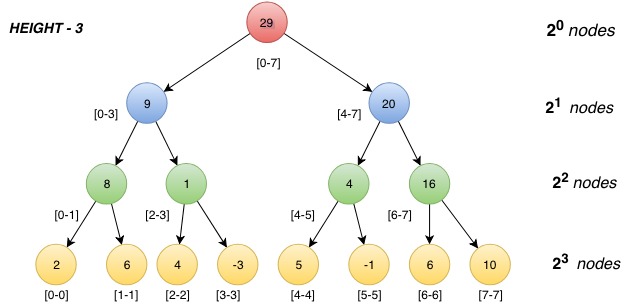
• Construction of a Segment tree :

1. Each node of the segment tree contains the sum of a range {say [L,R]} and its left child contains the sum of range [L, mid] and the right child contains the sum of range
   [mid + 1, R] where mid = (L+R)/2.
2. The root node contains the sum of range [0, n], thats is, the sum of complete array.
3. As we keep on dividing range of parent node into two halves onto its child nodes, eventually we will not be able to create more child nodes once the range of a node contains only one element, that is, with the range [i, i]. Therefore, the nodes containing the sum of a single element of array, will be the leaf nodes as its range can not be divided.
4. Now all the array elements will be present at the leaf nodes and number of leaf nodes in the tree will be equal to length of the array.

Now how do we store the tree?

We will store the tree in an array where the index of the left child of any parent node at i th index will be stored at index 2i+1 and the index of right node will be stored at index 2i+2.
All the leaf nodes will contain the elements of given array and the parents of these nodes will contain the sum of its left child and right child.

What will be the size of the array?
To answer this question we first need to know, how many nodes will be there in the complete tree.
Let us consider an array with length equal to perfect power of two to understand it more clearly.

int[] arr = {2, 6, 4, -3, 5, -1, 6, 10}

As at every next level, every node at current level is splitting into two nodes, hence the nodes at next level will be twice the nodes at current level.
0th level will contain 2^0 that is,  1 node which is root node.
1st level will contain 2^1 nodes.
2nd level will contain 2^2 nodes.
3rd level will contain 2^3 nodes.
.
.
.
last level will contain 2^height nodes.

Therefore, Total number of nodes = 2^0 + 2^1 + 2^2 + …. + 2^height
= 2^(height+1) – 1 { sum of a G.P.}
We know,
Height of a tree = log(n) to the base 2.
where, n = size of the given array.

Therefore, the total nodes = 2^((log n) +1) – 1.
As we store every node of the tree in an array, therefore,

the size of the segment array will be 2^((log n) +1) – 1.

int[] segArr = new int[2^((log n) +1) – 1];

Construction :

1. We start from root node going down deep in recursion and we set the values in postorder i.e after we set the values of its children.
2. For any node we call for its two children left and right with incrementing the pointer for segment array to 2*idx+1 and 2*idx+2 respectively, also we reduce the segment length for each child to half the range of its parent.
3. Whenever we encounter a leaf node which we get know when we have left limit = right limit, we straightaway put the value present at left/right in given array (since they both are equal for leaf we can use either of them) at the current index in the segment array. This would be our base case and we would return the value of this leaf node after we set it.
4. In case of an inner node, its value will be calculated in postorder by summing up the values of both of its child.

Range Sum Query :

Whenever we are given a query for finding out the sum of a given range (say [query_left, query_right]).
We keep these three points in mind:
(i) if the query range lies completely outside the segment of the current node we are currently present at, we return a value such that it does not contribute anything into our final answer because answer for the asked range lies in some other node(s).
(ii) if the query range lies completely inside the range of the current segment then we return the complete value of this segment because this segment will contribute everything to the asked range query.
(iii) if there is any overlap in the segment of the current node and the range of the query, we call for both of its children, as the current segment will contribute to the final answer but not completely.

Updation:

In updation we will be required to update the value at an index in the given array.
We start from the root node searching for the leaf node that contains the value of the asked index. Then in post order we correct the values of all those nodes which contains the updated index in their segment range.

When you run above program, you will get below output:

That’s all about Segment tree in java