If you want to practice data structure and algorithm programs, you can go through 100+ java coding interview questions.
In this post, we will see about how to count subtrees with Sum equal to target in binary tree
Problem
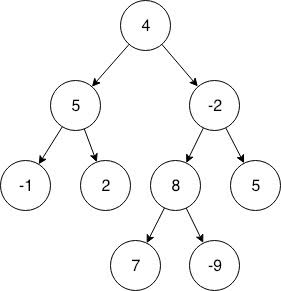
Given a Binary tree and an integer. You need to find the number of subtrees having the sum of all of its nodes equal to given Integer, that is, Target sum.
Solution
For solving this problem, we calculate the result in postorder while returning from recursion in which we return a Pair object which contains the sum of current subtree and count of subtrees having their sum equal to given sum.
So basically, we keep on recurring to child of the current node until we finally reach to a null node where we return an empty pair class object in which sum of current subtree is zero and also the count of subtrees with sum equal to target sum equal to zero.
Result of any node or the pair to be returned will be calculated using the pair objects returned from left child and right child of the current node.
There are two things we need to calculate for current node :
- (i) SUM : Sum of current node will be the summation of left subtree sum, right subtree sum and value of
current node. - (ii) Count : Count of subtrees with sum Equal to target sum will left count + right count and add one if the
overall sum of the current node is equal to target sum.
The time complexity of this algorithm would be similar to all other traversals like postorder, that is, O(n) , where ‘n’ is number of nodes in the tree.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 |
package BinaryTrees; public class SubtreesWithGivenSum { public static class Node { int data; // Data of current Node. Node left; // Pointer to left child Node. Node right; // Pointer to right child Node. public Node(int data) { this.data = data; } } public static class pair { /*number of subtrees with given target sum*/ int count; /* sum of the current subtree which includes the * sum of root of current subtree, left child * subtree and, right child subtree*/ int sum; public pair(int count, int sum) { this.count = count; this.sum = sum; } } public static void main(String[] args) { Node root = new Node(4); root. left = new Node(5); root. right = new Node(-2); root. left. left = new Node(-1); root. left. right = new Node(2); root. right. right = new Node(5); root. right. left = new Node(8); root. right. left. left = new Node(7); root. right. left. right = new Node(-9); System.out.println(solve(root, 6).count); } public static pair solve(Node node, int target) { if(node == null) { /* if current node is null, then its contribution to total * sum of a subtree will be zero and also it won't have * any subtree with sum equal to given target sum */ return new pair(0, 0); } /*calls for left and right subtree*/ pair left = solve(node.left, target); pair right = solve(node.right, target); /*sum of current subtree will be the sum of data of current node, * sum of left child subtree and, sum of right child subtree*/ int sum = left.sum + right.sum + node.data; int count = left.count + right.count; /* count of subtrees with target sum will be the sum of count * of subtrees on left with sum equal to target, count of * subtrees on right with sum equal to target, and one if * the current subtree has sum equal to target*/ if(sum==target) { count++; } return new pair(count, sum); } } |
That’s all about Count subtrees with Sum equal to target in binary tree.


