Table of Contents
If you want to practice data structure and algorithm programs, you can go through Java coding interview questions.
In this post, we will see about how to count all paths from top left to bottom right of MxN matrix.
Problem
We need to count all paths from top left to bottom right of MxN matrix. You can either move down or right.
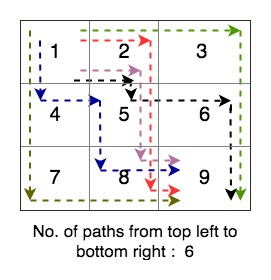
Solution
You can solve this problem using recursion.
Recursion
|
1 2 3 4 5 6 7 8 9 10 |
public int countMatrixPathsRec(int [][] matrix, int row, int col){ //base case // If you reach at last row or column then you have only one path to go if(row==matrix.length-1 || col==matrix[0].length-1){ return 1; } return countMatrixPathsRec(matrix, row+1, col) + countMatrixPathsRec(matrix, row, col+1); } |
Recursion will work fine but time complexity of this solution will be exponential as there are lots of overlapping subproblems here.
We can use dynamic programming to solve the problem. We won’t recompute any subproblem more than once.
Dynamic programming
Here is simple algorithm for dynamic programming solution.
- Initialize an array dp with matrix’s dimensions. This array will give us final count, once we reach to bottom right.
- Fill the first row with 1, as you can reach here from one direction(by going right)
- Fill the first column with 1 as well, as you can reach here from one direction(by going down).
- Iterate over all other rows and columns and use formula dp=dp[i-1][j] + dp[i][j-1], as you can reach here from two directions (By going right or By going down)
- return dp[matrix.length-1][matrix[0].length-1]
Here is a diagramtic illustration of the algorithm.
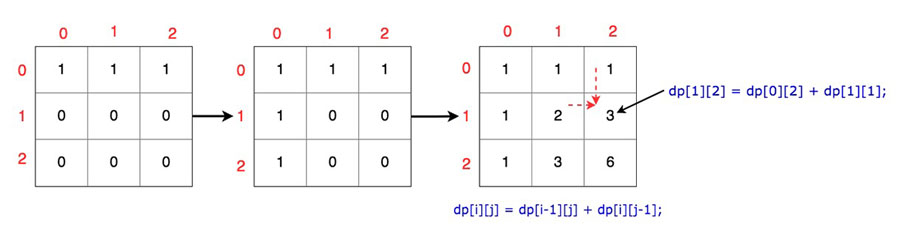
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
public int countMatrixPathsDynamicProgramming(int [][] matrix){ int dp [][] = new int[matrix.length][matrix[0].length]; // no of path for first row will be 1 as you can move only in one direction for (int i = 0; i <dp.length ; i++) { dp[0][i] = 1; } // no of path for first column will be 1 as you can move only in one direction for (int i = 0; i <dp.length ; i++) { dp[i][0] = 1; } for (int i = 1; i <dp.length ; i++) { for (int j = 1; j <dp.length ; j++) { dp[i][j] = dp[i-1][j] + dp[i][j-1]; } } return dp[matrix.length-1][matrix[0].length-1]; } |
Here is complete program to Count all paths from top left to bottom right of MxN matrix.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
package org.arpit.java2blog; public class CountMatrixPaths { public static void main(String[] args) { CountMatrixPaths cmp=new CountMatrixPaths(); int[][] matrix= { {1,2,3}, {4,5,6}, {7,8,9} }; int totalPathsRec = cmp.countMatrixPathsRec(matrix,0,0); System.out.println("Total paths to reach top left to bottom right using recursion: "+totalPathsRec); int totalPaths = cmp.countMatrixPathsDynamicProgramming(matrix); System.out.println("Total paths to reach top left to bottom right using DP: "+totalPaths); } public int countMatrixPathsRec(int [][] matrix, int row, int col){ //base case // If you reach at last row or column then you have only one path to go if(row==matrix.length-1 || col==matrix[0].length-1){ return 1; } return countMatrixPathsRec(matrix, row+1, col) + countMatrixPathsRec(matrix, row, col+1); } public int countMatrixPathsDynamicProgramming(int [][] matrix){ int dp [][] = new int[matrix.length][matrix[0].length]; // no of path for first row will be 1 as you can move only in one direction for (int i = 0; i <dp.length ; i++) { dp[0][i] = 1; } // no of path for first column will be 1 as you can move only in one direction for (int i = 0; i <dp.length ; i++) { dp[i][0] = 1; } for (int i = 1; i <dp.length ; i++) { for (int j = 1; j <dp.length ; j++) { dp[i][j] = dp[i-1][j] + dp[i][j-1]; } } return dp[matrix.length-1][matrix[0].length-1]; } } |
Here is output of the above program.
Total paths to reach top left to bottom right using DP: 6
That’s all about counting all paths from top left to bottom right of MxN matrix.


