Table of Contents
If you want to practice data structure and algorithm programs, you can go through 100+ java coding interview questions.
1. Introduction
In this article, we will explore the concept of PostOrder traversal in binary trees, focusing on its implementation in Java. In computer science, a binary tree is a foundational data structure, and traversing it is a fundamental technique. Among the various traversal methods, PostOrder traversal is widely used due to its applications across a range of algorithms and operations.
2. What is PostOrder Traversal?
3. Process of PostOrder Traversal
- Traverse the
left subtreein PostOrder. - Traverse the
right subtreein PostOrder. Visitthe node.
4. Implementation
There can be two ways of implementing it:
- Recursive
- Iterative
4.1 Recursive Solution
Recursive solution is very straight forward. Below diagram will make you understand recursion better.
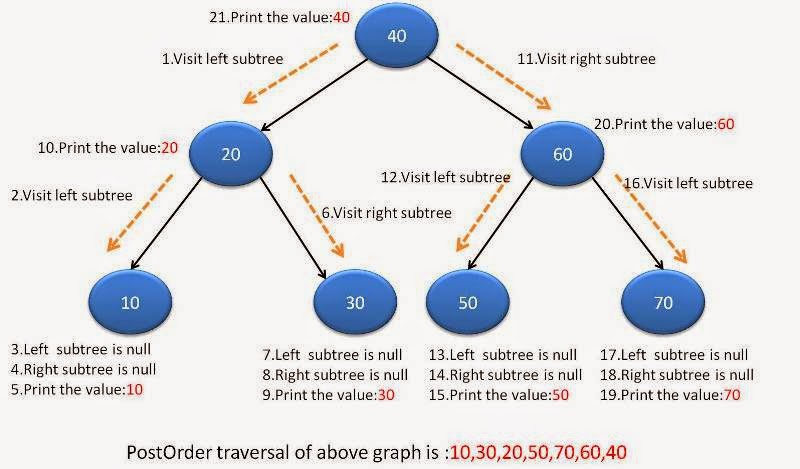
Code for recursion will be:
|
1 2 3 4 5 6 7 8 9 10 11 |
// Recursive Solution public void postOrder(TreeNode root) { if(root != null) { postOrder(root.left); postOrder(root.right); //Visit the node by Printing the node data System.out.printf("%d ",root.data); } } |
The time complexity for recursive approach is O(n), where n is the number of nodes in the binary tree. This is because each node in the tree is visited exactly once.
The space complexity is O(h), where h is the height of the tree. This complexity arises from the use of the call stack to handle recursion. In the worst case (a skewed tree), the height of the tree can become n, making the space complexity O(n).
4.2 Iterative Solution
Steps for iterative solution:
- Create an empty stack
sand setcurrentNode =root. - while
currentNodeis not NULL Do following- Push
currentNode 's right childand thencurrentNodeto stacks - Set
currentNode=currentNode.left
- Push
- Pop a node from stack
sand set it tocurrentNode- If the popped node has a
right childand the right child is at top of stack, thenremovethe right child from stack, push thecurrentNodeback and setcurrentNodeascurrentNode 's right child. - Else print
currentNode's dataand setcurrentNodeas NULL.
- If the popped node has a
- Repeat steps 2 and 3 while stack is not empty.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
// Iterative solution public void postorderIter( TreeNode root) { if( root == null ) return; Stack<TreeNode> s = new Stack<TreeNode>( ); TreeNode current = root; while( true ) { if( current != null ) { if( current.right != null ) s.push( current.right ); s.push( current ); current = current.left; continue; } if( s.isEmpty( ) ) return; current = s.pop( ); if( current.right != null && ! s.isEmpty( ) && current.right == s.peek( ) ) { s.pop( ); s.push( current ); current = current.right; } else { System.out.print( current.data + " " ); current = null; } } } |
The space complexity is O(h), where h is the height of the tree. This complexity arises from the use of an explicit stack to keep track of nodes. In the worst case (a skewed tree), the height of the tree can become n, making the space complexity O(n).
5. Complete Java Program
Let’s say our binary tree is:
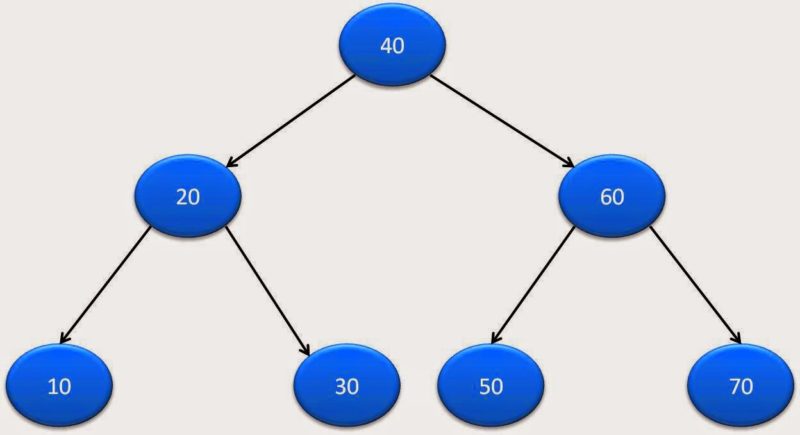
Here is complete java program for PostOrder traversal:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 |
import java.util.Stack; public class BinaryTreePostOrder { public static class TreeNode { int data; TreeNode left; TreeNode right; TreeNode(int data) { this.data=data; } } // Recursive Solution public void postOrder(TreeNode root) { if(root != null) { postOrder(root.left); postOrder(root.right); //Visit the node by Printing the node data System.out.printf("%d ",root.data); } } // Iterative solution public void postorderIter( TreeNode root) { if( root == null ) return; Stack<TreeNode> s = new Stack<TreeNode>( ); TreeNode current = root; while( true ) { if( current != null ) { if( current.right != null ) s.push( current.right ); s.push( current ); current = current.left; continue; } if( s.isEmpty( ) ) return; current = s.pop( ); if( current.right != null && ! s.isEmpty( ) && current.right == s.peek( ) ) { s.pop( ); s.push( current ); current = current.right; } else { System.out.print( current.data + " " ); current = null; } } } public static void main(String[] args) { BinaryTreePostOrder bi=new BinaryTreePostOrder(); // Creating a binary tree TreeNode rootNode=createBinaryTree(); System.out.println("Using Recursive solution:"); bi.postOrder(rootNode); System.out.println(); System.out.println("-------------------------"); System.out.println("Using Iterative solution:"); bi.postorderIter(rootNode); } public static TreeNode createBinaryTree() { TreeNode rootNode =new TreeNode(40); TreeNode node20=new TreeNode(20); TreeNode node10=new TreeNode(10); TreeNode node30=new TreeNode(30); TreeNode node60=new TreeNode(60); TreeNode node50=new TreeNode(50); TreeNode node70=new TreeNode(70); rootNode.left=node20; rootNode.right=node60; node20.left=node10; node20.right=node30; node60.left=node50; node60.right=node70; return rootNode; } } |
Run above program and you will get following output:
10 30 20 50 70 60 40
————————-
Using Iterative solution:
10 30 20 50 70 60 40
6. Conclusion
In this article, we covered about Binary tree PostOrder traversal and its implementation. We have done traversal using two approaches: Iterative and Recursive. We also discussed about time and space complexity for the PostOrder traversal.
Java Binary tree tutorial
- Binary tree in java
- Binary tree preorder traversal
- Binary tree postorder traversal
- Binary tree inorder traversal
- Binary tree level order traversal
- Binary tree spiral order traversal
- Binary tree reverse level order traversal
- Binary tree boundary traversal
- Print leaf nodes of binary tree
- Count leaf nodes in binary tree
- get maximum element in binary tree
- Print all paths from root to leaf in binary tree
- Print vertical sum of binary tree in java
- Get level of node in binary tree in java
- Lowest common ancestor(LCA) in binary tree in java



What happens when the last left node does not have any children?