If you want to practice data structure and algorithm programs, you can go through 100+ java coding interview questions.
Table of Contents
Graph traversal Algorithms
In DFS,  You start with  an un-visited node and start picking an adjacent node, until you have no choice, then you backtrack until you have another choice to pick a node, if not, you select another un-visited node.
DFS can be implemented in two ways.
- Recursive
- Iterative
Iterative
Depth-first search can be implemented using iterative approach.
Let see with the help of example:
Let see with the help of example:
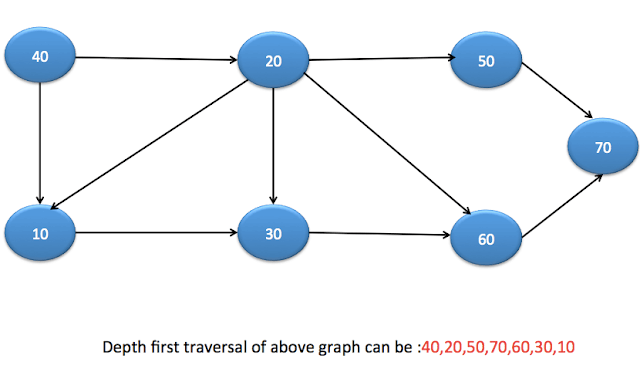
We start with node 40. It then visits node 20, node 50, node 70 respectively as they are directly connected. After that, it backtracks to node 20 and visited node 60, node 30 and node 10 respectively.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
// Iterative DFS using stack public void dfsUsingStack(Node node) { Stack<Node> stack=new Stack<Node>(); stack.add(node); while (!stack.isEmpty()) { Node element=stack.pop(); if(!element.visited) { System.out.print(element.data + " "); element.visited=true; } List<Node> neighbours=element.getNeighbours(); for (int i = 0; i < neighbours.size(); i++) { Node n=neighbours.get(i); if(n!=null && !n.visited) { stack.add(n); } } } } |
Recursive
Depth first search can be implemented using recursion too. We do not need to maintain external stack, it will be taken care by recursion.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
// Recursive DFS public void dfs(Node node) { System.out.print(node.data + " "); List neighbours=node.getNeighbours(); node.visited=true; for (int i = 0; i < neighbours.size(); i++) { Node n=neighbours.get(i); if(n!=null && !n.visited) { dfs(n); } } } |
Java DFS Example
There are two ways to represent a graph.
-
- Using Neighbours list
- Using Adjacency Matrix
Using Neighbours list
In this, you can have List<Node> as neighbours in Node class as below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
static class Node { int data; boolean visited; List<Node> neighbours; Node(int data) { this.data=data; this.neighbours=new ArrayList<>(); } public void addneighbours(Node neighbourNode) { this.neighbours.add(neighbourNode); } public List getNeighbours() { return neighbours; } public void setNeighbours(List neighbours) { this.neighbours = neighbours; } } |
Here is the complete java program for DFS implementation for iterative as well as recursive method.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 |
package org.arpit.java2blog; import java.util.ArrayList; import java.util.List; import java.util.Stack; public class DepthFirstSearchExampleNeighbourList { static class Node { int data; boolean visited; List<Node> neighbours; Node(int data) { this.data=data; this.neighbours=new ArrayList<>(); } public void addneighbours(Node neighbourNode) { this.neighbours.add(neighbourNode); } public List<Node> getNeighbours() { return neighbours; } public void setNeighbours(List<Node> neighbours) { this.neighbours = neighbours; } } // Recursive DFS public void dfs(Node node) { System.out.print(node.data + " "); List<Node> neighbours=node.getNeighbours(); node.visited=true; for (int i = 0; i < neighbours.size(); i++) { Node n=neighbours.get(i); if(n!=null && !n.visited) { dfs(n); } } } // Iterative DFS using stack public void dfsUsingStack(Node node) { Stack<Node> stack=new Stack<Node>(); stack.add(node); while (!stack.isEmpty()) { Node element=stack.pop(); if(!element.visited) { System.out.print(element.data + " "); element.visited=true; } List<Node> neighbours=element.getNeighbours(); for (int i = 0; i < neighbours.size(); i++) { Node n=neighbours.get(i); if(n!=null && !n.visited) { stack.add(n); } } } } public static void main(String arg[]) { Node node40 =new Node(40); Node node10 =new Node(10); Node node20 =new Node(20); Node node30 =new Node(30); Node node60 =new Node(60); Node node50 =new Node(50); Node node70 =new Node(70); node40.addneighbours(node10); node40.addneighbours(node20); node10.addneighbours(node30); node20.addneighbours(node10); node20.addneighbours(node30); node20.addneighbours(node60); node20.addneighbours(node50); node30.addneighbours(node60); node60.addneighbours(node70); node50.addneighbours(node70); DepthFirstSearchExampleNeighbourList dfsExample = new DepthFirstSearchExampleNeighbourList(); System.out.println("The DFS traversal of the graph using stack "); dfsExample.dfsUsingStack(node40); System.out.println(); // Resetting the visited flag for nodes node40.visited=false; node10.visited=false; node20.visited=false; node30.visited=false; node60.visited=false; node50.visited=false; node70.visited=false; System.out.println("The DFS traversal of the graph using recursion "); dfsExample.dfs(node40); } } |
When you run above program, you will get below output
|
1 2 3 4 5 6 |
The DFS traversal of the graph using stack 40 20 50 70 60 30 10 The DFS traversal of the graph using recursion 40 10 30 60 70 20 50 |
Using Adjacency Matrix
Adjacency_matrix is used to find the connection between two nodes.
if adjacency_matrix[i][j]==1, then nodes at index i and index j are connected
Below diagram will help you to understand adjacency matrix.
Create DepthFirstSearchExample.java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 |
package org.arpit.java2blog.graph; import java.util.ArrayList; import java.util.Stack; public class DepthFirstSearchExample { static ArrayList<Node> nodes=new ArrayList<>(); static class Node { int data; boolean visited; Node(int data) { this.data=data; } } // find neighbors of node using adjacency matrix // if adjacency_matrix[i][j]==1, then nodes at index i and index j are connected public ArrayList<Node> findNeighbours(int adjacency_matrix[][],Node x) { int nodeIndex=-1; ArrayList<Node> neighbours=new ArrayList<>(); for (int i = 0; i < nodes.size(); i++) { if(nodes.get(i).equals(x)) { nodeIndex=i; break; } } if(nodeIndex!=-1) { for (int j = 0; j < adjacency_matrix[nodeIndex].length; j++) { if(adjacency_matrix[nodeIndex][j]==1) { neighbours.add(nodes.get(j)); } } } return neighbours; } // Recursive DFS public void dfs(int adjacency_matrix[][], Node node) { System.out.print(node.data + " "); ArrayList<Node> neighbours=findNeighbours(adjacency_matrix,node); node.visited=true; for (int i = 0; i < neighbours.size(); i++) { Node n=neighbours.get(i); if(n!=null && !n.visited) { dfs(adjacency_matrix,n); } } } // Iterative DFS using stack public void dfsUsingStack(int adjacency_matrix[][], Node node) { Stack<Node> stack=new Stack<>(); stack.add(node); while (!stack.isEmpty()) { Node element=stack.pop(); if(!element.visited) { System.out.print(element.data + " "); element.visited=true; } ArrayList<Node> neighbours=findNeighbours(adjacency_matrix,element); for (int i = 0; i < neighbours.size(); i++) { Node n=neighbours.get(i); if(n!=null &&!n.visited) { stack.add(n); } } } } public static void main(String arg[]) { Node node40 =new Node(40); Node node10 =new Node(10); Node node20 =new Node(20); Node node30 =new Node(30); Node node60 =new Node(60); Node node50 =new Node(50); Node node70 =new Node(70); nodes.add(node40); nodes.add(node10); nodes.add(node20); nodes.add(node30); nodes.add(node60); nodes.add(node50); nodes.add(node70); int adjacency_matrix[][] = { {0,1,1,0,0,0,0}, // Node 1: 40 {0,0,0,1,0,0,0}, // Node 2 :10 {0,1,0,1,1,1,0}, // Node 3: 20 {0,0,0,0,1,0,0}, // Node 4: 30 {0,0,0,0,0,0,1}, // Node 5: 60 {0,0,0,0,0,0,1}, // Node 6: 50 {0,0,0,0,0,0,0}, // Node 7: 70 }; DepthFirstSearchExample dfsExample = new DepthFirstSearchExample(); System.out.println("The DFS traversal of the graph using stack "); dfsExample.dfsUsingStack(adjacency_matrix, node40); System.out.println(); clearVisitedFlags(); System.out.println("The DFS traversal of the graph using recursion "); dfsExample.dfs(adjacency_matrix, node40); } public static void clearVisitedFlags() { for (int i = 0; i < nodes.size(); i++) { nodes.get(i).visited=false; } } } |
When you run above program, you will get below output
|
1 2 3 4 5 6 |
The DFS traversal of the graph using stack 40 20 50 70 60 30 10 The DFS traversal of the graph using recursion 40 10 30 60 70 20 50 |
Please go through data structure and algorithm interview programs for more such programs.
Was this post helpful?
Let us know if this post was helpful. Feedbacks are monitored on daily basis. Please do provide feedback as that\'s the only way to improve.
oh, so easy to understand, thanks!