In this post, we will see how to convert infix to postfix expression in java. This is an important problem related to Stack Data Structure
Table of Contents
Let us quickly look into Infix and Postfix expression:
Infix expressions are the expression where operators are written in between every pair of operands. It is the usual way to write an expression. For Ex: An expression like A + B is Infix.
Postfix expressions are the expressions where operands precede operators. Here operators are written after operands. The Expression AB+ is Postfix and is the Postfix representation of the above shown A+B. The evaluation order is from left to right.
Why we use Postfix expression?
The expressions we (humans) write are Infix Expression, but for the machines to understand these expression they need to be converted. The compiler scans an expression from left to right. If an infix expression such as A*(B+C) is provided, the compiler will scan the expression to evaluate B+C then scan again to multiply the result with A. This results in multiple scanning. So, it is recommended to use Postfix notations which for the given expression is: ABC+* . A compiler can then easily evaluate the result in one go.
Now how is the conversion done? We will look into the algorithm for this along with an example.
Conversion Algorithm
We will use two Stacks : One for Operators (Character), One for Operands (String). The Operand stack will contain the resultant Postfix expression after traversing string. The Infix expression will be given as a String input. We will take decisions when we encounter Parentheses, Operators and Operands. So the steps are:
-
Step 1:We will iterate throughout the String length. For each character, there are three cases to consider :- 1. If the Current character is a Operand.
- 2. If the character is a Open or Close Parentheses.
- 3. If the character is an Operator.
-
Step 2:If the Character at each iteration is a Operand. We simply push it into the operand or Postfix stack. -
Step 3:If the character encountered is :'(', i.e. Opening Parentheses, we push it into Operator Stack. -
Step 4:Now, if we encounter')'i.e. Closing Parenthesis, we are going to pop the elements out of Operator Stack until we get the opening'('. For each operator we pop its two operands and process them. -
Step 5:The process for each operator is : We pop two elements from Postfix or operand Stack we concatenate them in reverse order with its operator and add the result again to Postfix stack for future evaluation until we get the total Postfix expression. -
Step 6:Now if we get an Operator as the current character, we check whether the precedence of current operator is lower than the operator present at top of the stack. If the condition is true, we pop the operator present at the top and process its operands following Step 5. Then we push the current operator into the stack. -
Step 7:At last after traversing the whole string if still we are left with any operators we pop them and continue Step 5 until the Operator Stack is empty. At last, the Postfix stack will have only one element which will be our resultant Postfix Expression.
Note: The Precedence of * and / are equal and higher than + and - operation.
Let us understand this Algorithm with an example:
Consider the Infix : A * (B-C) / D + E
We take 2 Stacks: Operator and Postfix, and do the following steps:
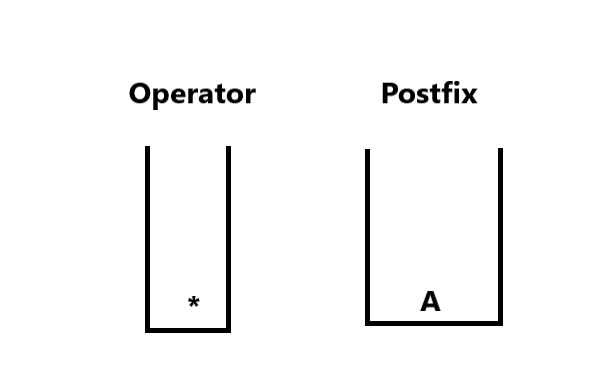
1. We start iterating through each character (ignoring the spaces). At i=0, char = ‘A’ an Operand. We push it into Postfix stack. At i=1, char = ‘*’ an operator, we push it into operator stack. The stacks look like:
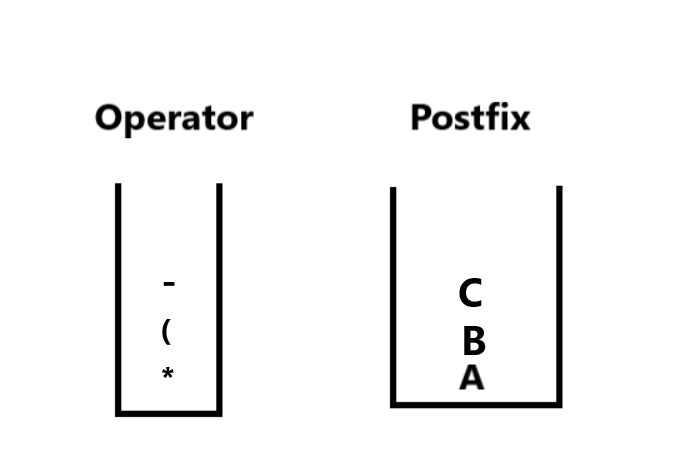
2. We continue at i=2, char = ‘(‘ , an opening parenthesis we push it into operator stack, at i=3, char =’B’ we push it into Postfix stack . At i=4, char = ‘-‘ we push it into Operator stack, at i=5, char = ‘C’ we push into the Postfix stack. The stacks now look like:
3. We continue iterating, at i=6; char =’)’ i.e. a Closing Parenthesis, so now we follow Step 4 and Step 5 of the algorithm . We pop elements from operator stack until we get the Opening Parenthesis. Then, we pop two elements from Postfix stack (C and B), concatenate them in reverse order with the operator in reverse order (BC-) and add the result into the Postfix stack again. Then we pop ‘)’. The stacks now look like :
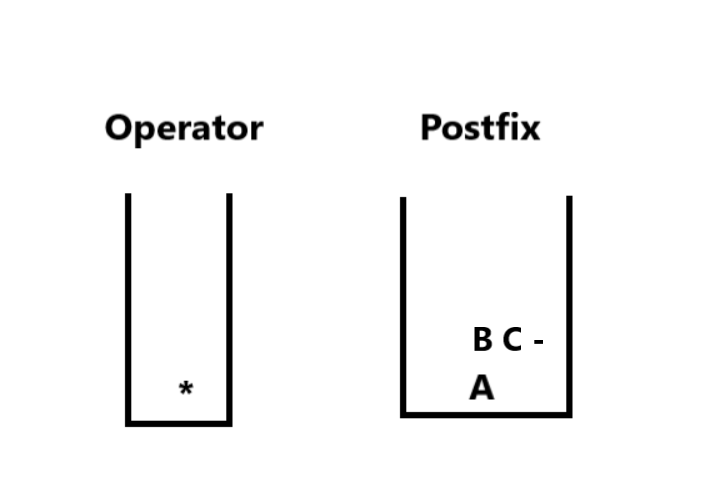
BC- is an operand in Postfix Stack.4. Then at i=7, char = /, an operator, we need to add it to our Operator stack but before doing it we check whether there is an operator in the stack with precedence higher or equal to current operator . There is * operator in stack with precedence equal to / ,so we process it following Step 5. Then push / operator. So we pop * and add it with operands (A and BC- ) using Step 5. The stacks now look like :
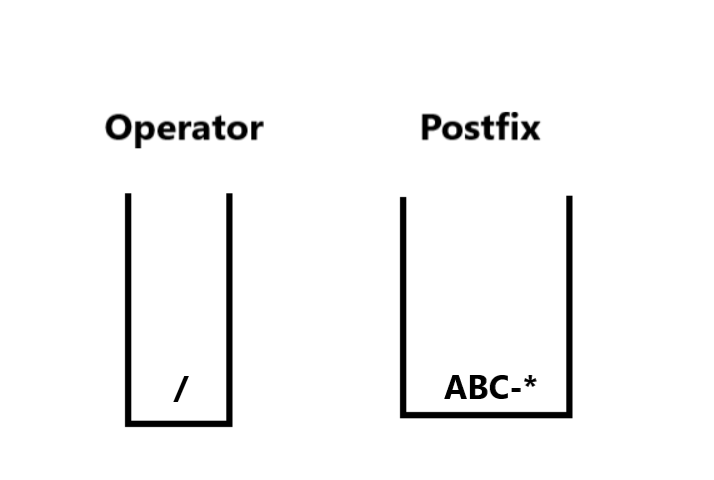
5. We continue, at i=8, char =D, we push it into Postfix stack. At i=9, we have + operator, we again check the stack for any operator with greater precedence. / has higher precedence, so we process it first like shown above using Step 5 then push + into the Stack. The stacks now are:
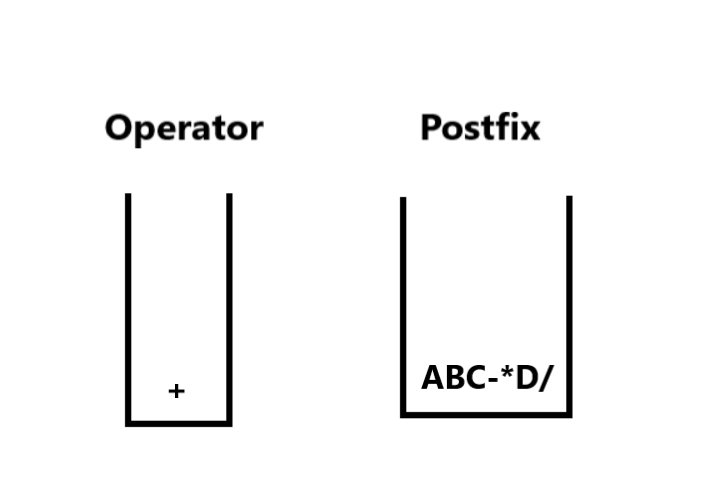
6. Finally at i=10, we have char = E, so we push it in the postfix stack.
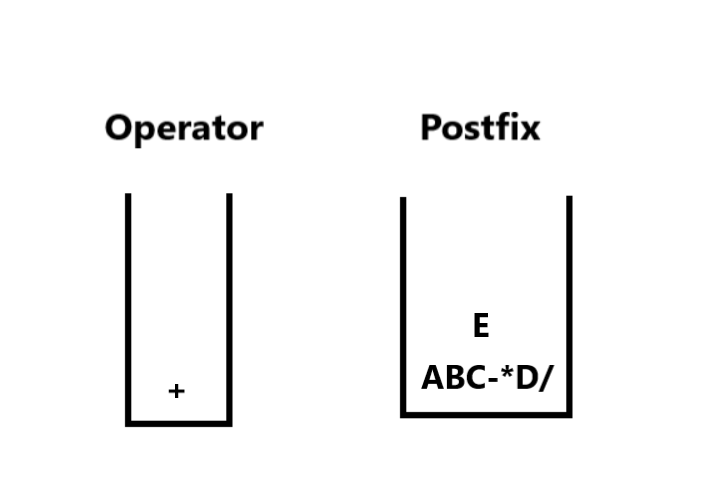
7. Now this is an important point, After traversing the string if there are still any operators left in the stack, we process them repeating Step 5 until we get the final expression. In this case, after iterating the string the + is still remaining in Operator Stack. After processing the last operator the stacks now look like :
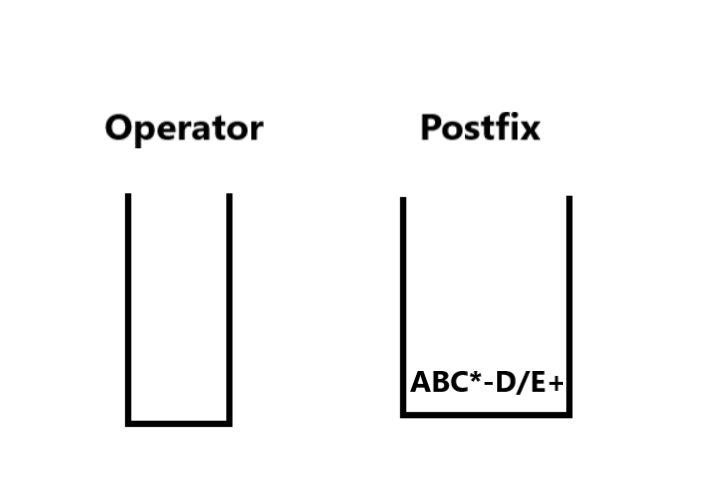
Note:The Postfix stack at last will hold the Postfix expression and will be the only element.
Implementation
Now let us look at the implementation code in JAVA:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 |
import java.util.*; public class InfixtoPostfix { public static int precedence(char ch) { if(ch=='+' || ch=='-') return 1; else if(ch=='*' || ch=='/') return 2; // * and / divide have higher precedence. return 0; } public static String convertToPostfix(String exp) { Stack<Character> operators = new Stack<>(); Stack<String> postFix = new Stack<>(); for(int i=0;i<exp.length();i++) { char ch=exp.charAt(i); // current character. if(ch=='(') operators.push(ch); else if((ch>='a' && ch<='z') || (ch>='A' && ch<='Z')) postFix.push(ch+""); else if(ch==')') { while(operators.peek()!= '(') { // STEP 5 of Algorithm. char op = operators.pop(); String first = postFix.pop(); // get the two operands. String second = postFix.pop(); String new_postFix = second+first+op; // add them in reverse order. postFix.push(new_postFix); // push the result to postFix stack again. } operators.pop(); // pop '(' from stack. } // We do the same thing if we get an operator as the current character. else if(ch=='+' || ch=='-' || ch== '*' || ch== '/') { // check precedence of each operator with top of the stack and process them. while(operators.size()>0 && operators.peek()!='(' && precedence(ch) <= precedence(operators.peek())) { char op = operators.pop(); String first = postFix.pop(); String second = postFix.pop(); String new_postFix = second+first+op; postFix.push(new_postFix); } operators.push(ch); } } // If the operator stack still has some elements in it process them too Repeat Step 5. while(operators.size()>0) { char op = operators.pop(); String first = postFix.pop(); String second = postFix.pop(); String new_postFix = second+first+op; postFix.push(new_postFix); } return postFix.pop(); // return resultant Postfix. } public static void main(String args[]) { // We pass Uppercase Infix String infixExpression = "A*(B-C)/D+E"; System.out.println("The Infix Expression is: "+infixExpression); String result = convertToPostfix(infixExpression); System.out.println("The Postfix of the given Infix Expression is: "+result); System.out.println(); //We also check for Lowercase Infix infixExpression = "a*(b-c+d)/e"; System.out.println("The Infix Expression is: "+infixExpression); result = convertToPostfix(infixExpression); System.out.println("The Postfix of the given Infix Expression is: "+result); } } |
Output:
|
1 2 3 4 5 6 7 |
The Infix Expression is: A*(B-C)/D+E The Postfix of the given Infix Expression is: ABC-*D/E+ The Infix Expression is: a*(b-c+d)/e The Postfix of the given Infix Expression is: abc-d+*e/ |
This the output for the above discussed example and a sample. Let us look into the the time complexity of our approach.
Time Complexity: We do a single traversal of the string to convert it into Postfix expression so the time complexity is O(n) , n is the length of Infix Expression.
That’s all about how to convert infix to postfix in java. You can try out this with various examples and execute this code for a clear idea.



