If you want to practice data structure and algorithm programs, you can go through Java coding interview questions.
In this post, we will see about Lowest Common Ancestor for n-ary Tree.
Problem
Given a n-ary tree also known as a Generic Tree and also two nodes. You need to find the Lowest common ancestor of the two given nodes.
A n-ary tree is basically a tree with any number of children.
Lowest Common Ancestor is the node which is the common ancestor for both the nodes which is closest to them or we can say, farthest from root.
Consider the Given Tree,
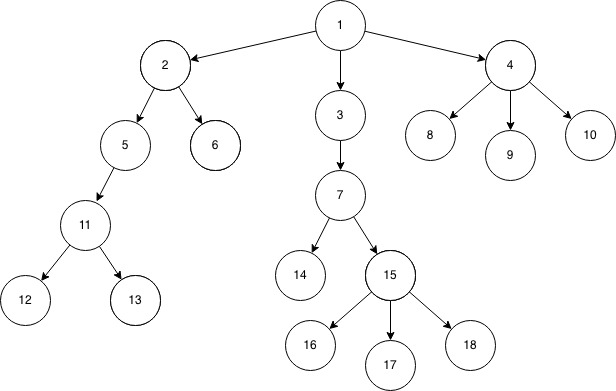
Input Format:
In the first line, given n, the number of nodes, following that n-1 lines contains two integers, the first one representing parent, second one is the child.
After that, given two Integers, whose LCA is to be found.
For Eg:-
18
1 2
1 3
1 4
2 5
2 6
3 7
4 8
4 9
4 10
5 11
11 12
11 13
7 14
7 15
15 16
15 17
15 18
6 13
Output : 2
Solution
Approach – I :
In this approach, we will basically use the find node algorithm, we start with root node, keep searching for both of the given nodes whose LCA id to be found say(u, v).
- There are two cases When a node will be LCA :
- (i) When itself is one of the node i.e equal to u or v, and other node falls in the subtree of its children.
- (ii) When both the nodes falls in the DIFFERENT subtrees of its children, if they fall in the
same subtree of its child, then this node might not be the LCA.
- So we start from root node, keep on recurring in preorder, searching for u and v. If we find any node of u and v then we return true, as this might be the LCA, even though we have a different condition for considering it as the LCA which we will see later.
- When we recur for children of any node, we keep a counter of how many child are giving a true as result, because :
- (i) If exactly Two of its children return true, this means that the current node is the LCA (As discussed in the second case).
- (ii) If one of its child return true and it itself is one of the node whose LCA to be found then this node is LCA (As discussed in the First case).
As we are setting LCA in postorder, we need to make sure that we set it only once.
As we are recurring in preorder, visiting every node, so the time complexity of this approach would be O(n).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 |
package org.arpit.java2blog; import java.util.ArrayList; import java.util.Scanner; public class LCAnFind { public static void main(String[] args) { Scanner scn = new Scanner(System.in); int numNodes = scn.nextInt(); @SuppressWarnings("unchecked") ArrayList<Integer>[] tree = new ArrayList[numNodes + 1]; for (int i = 0; i < tree.length; i++) { tree[i] = new ArrayList<>(); } // for a tree, edges are always equal to nodes-1 as it does not // have any cycle. int edges = numNodes - 1; while (edges-- > 0) { int parent = scn.nextInt(); int child = scn.nextInt(); tree[parent].add(child); } getLCA(1, tree, scn.nextInt(), scn.nextInt()); System.out.println("Output: "+lca); } static int lca = -1; public static boolean getLCA(int node, ArrayList<Integer>[] tree, int u, int v) { /* if current node is equal to one of the nodes whose lca we are finding, then it is a potential candidate for being the lca. */ boolean self = node == u || node == v ? true : false; int count = 0; /* recurring for every child. and keeping a count of result of how many times we are getting true. */ for (int child : tree[node]) { if (getLCA(child, tree, u, v)) { count++; } } /* this is the main check, if current node itself is one of the node whose lca is to be found and its getting true from any of its child, then surely it is LCA of given nodes. also, if we get true from exactly two sides, this means that current node is the node after which the path for both nodes diverge, and hence it is the LCA for given nodes. */ if (((self && count == 1) || (count == 2))) { /* lca will be set only once, as the parent of lca will have the count==2 condition as true, but that is not the correct answer. */ if (lca == -1) { lca = node; } return true; } /* current node will return true only if either the current node is one of the given nodes, or one of its children return true for count == 2, we already handled it while setting LCA. */ return self || count == 1; } } |
Approach – II :
This approach also solves the give problem in linear time i.e with the worst time complexity of O(n).
We basically use Root to node path to find out the LCA of two nodes.
- Lets first discuss how we find root to node path :
- We keep on traversing the tree in preorder basically looking for the node whose path we are currently finding.
- Once we find the node, there is no need for further calls for siblings or for child, we will return true and for stopping those further calls, we check if we already got a true already, if yes, then this means that we already found the node.
- We add the node into our path and while backtracking in postorder, we add only one node at a level, because if we keep adding the nodes in postorder without any check, then it is more likely that we will also add the sibling for a node whose root to node path we are actually finding.
- Now after we got our root to node path, we will traverse both the paths starting from extreme right end for both, and keep moving until we get a different node on both pointers, this means that the node which we are currently at is the node at which the path for both given nodes(whose LCA is to be found) are diverged and hence the previous node is the LCA of both nodes.
123456789package org.arpit.java2blog;</li></ul><p>import java.util.ArrayList;import java.util.HashMap;import java.util.Scanner;</p><p>public class LCAnRTNP {</p><pre>[[code]]czozMTQ1OlwicHVibGljIHN0YXRpYyBjbGFzcyBOb2RlIHsKCiAgICBpbnQgdmFsOwoKICAgIC8vIGFzIGl0cyBhIEstYXJ5IHRyZWV7WyYqJl19LCBTbyB3ZSBtYWtlIGEgdmFyaWFibGUgYXJyYXkgdG8gc3RvcmUgaXRzIGNoaWxkcmVuLgogICAgQXJyYXlMaXN0Jmx0O0ludGVnZXtbJiomXX1yJmd0OyBjaGlsZHJlbiA9IG5ldyBBcnJheUxpc3QmbHQ7Jmd0OygpOwoKICAgIC8vIGNvbnN0cnVjdG9yLGluaXRpYWxpemluZyB0e1smKiZdfWhlIG5vZGUgdmFsdWUgYW5kCiAgICBwdWJsaWMgTm9kZShpbnQgdmFsKSB7CiAgICAgICAgdGhpcy52YWwgPSB2YWw7CiAgICAgICB7WyYqJl19IHRoaXMuY2hpbGRyZW4gPSBuZXcgQXJyYXlMaXN0Jmx0OyZndDsoKTsKICAgIH0KCn0KCnN0YXRpYyBIYXNoTWFwJmx0O0ludGVnZXtbJiomXX1yLCBOb2RlJmd0OyBub2RlTWFwID0gbmV3IEhhc2hNYXAmbHQ7Jmd0OygpOwpzdGF0aWMgTm9kZSByb290OwoKcHVibGljIHN0YXRpe1smKiZdfWMgdm9pZCBtYWluKFN0cmluZ1tdIGFyZ3MpIHsKCiAgICBTY2FubmVyIHNjbiA9IG5ldyBTY2FubmVyKFN5c3RlbS5pbik7CgogICB7WyYqJl19IGludCBudW1ub2RlcyA9IHNjbi5uZXh0SW50KCk7CgogICAgZm9yIChpbnQgaSA9IDA7IGkgJmx0Oz0gbnVtbm9kZXM7IGkrKykge3tbJiomXX0KICAgICAgICBub2RlTWFwLnB1dChpLCBuZXcgTm9kZShpKSk7CiAgICB9CgogICAgcm9vdCA9IG5vZGVNYXAuZ2V0KDEpOwoKICAge1smKiZdfSBpbnQgZWRnZXMgPSBudW1ub2RlcyAtIDE7CgogICAgd2hpbGUgKGVkZ2VzLS0gJmd0OyAwKSB7CiAgICAgICAgaW50IHBhcmVudCB7WyYqJl19PSBzY24ubmV4dEludCgpOwogICAgICAgIGludCBjaGlsZCA9IHNjbi5uZXh0SW50KCk7CgogICAgICAgIC8vIHN0b3JpbmcgY2hpbHtbJiomXX1kIGluIHRoZSBhcnJheWxpc3Qgb2YgdGhlIHBhcmVudC4KICAgICAgICBBcnJheUxpc3QmbHQ7SW50ZWdlciZndDsgY2hpbGRyZW4ge1smKiZdfT0gbm9kZU1hcC5nZXQocGFyZW50KS5jaGlsZHJlbjsKICAgICAgICBjaGlsZHJlbi5hZGQoY2hpbGQpOwoKICAgIH0KCiAgICBnZXR7WyYqJl19TENBKHNjbi5uZXh0SW50KCksIHNjbi5uZXh0SW50KCkpOwoKfQoKcHVibGljIHN0YXRpYyB2b2lkIGdldExDQShpbnQgbm9kZTEsIHtbJiomXX1pbnQgbm9kZTIpIHsKCiAgICAvLyByb290IHRvIG5vZGUgcGF0aCBmb3Igbm9kZTEKICAgIEFycmF5TGlzdCZsdDtJbnRlZ2VyJmd0e1smKiZdfTsgcGF0aDEgPSBuZXcgQXJyYXlMaXN0Jmx0OyZndDsoKTsKICAgIHJvb3RUb05vZGVQYXRoKHJvb3QsIHBhdGgxLCBub2RlTWFwLmd7WyYqJl19ZXQobm9kZTEpKTsKICAgIHBhdGgxLmFkZChyb290LnZhbCk7CiAgICAvLyByb290IHRvIG5vZGUgcGF0aCBmb3Igbm9kZTIKICAgIHtbJiomXX1BcnJheUxpc3QmbHQ7SW50ZWdlciZndDsgcGF0aDIgPSBuZXcgQXJyYXlMaXN0Jmx0OyZndDsoKTsKICAgIHJvb3RUb05vZGVQYXRoe1smKiZdfShyb290LCBwYXRoMiwgbm9kZU1hcC5nZXQobm9kZTIpKTsKICAgIHBhdGgyLmFkZChyb290LnZhbCk7CgogICAgU3lzdGVtLm91dC57WyYqJl19cHJpbnRsbihwYXRoMSArIFxcXCJcXFxcblxcXCIgKyBwYXRoMik7CgogICAgaW50IHAxID0gcGF0aDEuc2l6ZSgpIC0gMTsKICAgIGludCBwMntbJiomXX0gPSBwYXRoMi5zaXplKCkgLSAxOwoKICAgIGludCBwcmV2TWF0Y2hpbmdOb2RlID0gLTE7CgogICAgLyoKICAgICAqIFdlIHN0YXJ0e1smKiZdfSB0d28gcG9pbnRlcnMgZm9yIHR3byBwYXRocyBpLmUuIG9uZSBmb3IgZWFjaCBub2RlLgogICAgICogIHdlIHdpbGwgc3RhcnQgZnJ7WyYqJl19b20gZXh0cmVtZSByaWdodCwga2VlcCBtb3ZpbmcgYm90aCAKICAgICAqIHBvaW50ZXJzIHRvd2FyZHMgbGVmdCB1bnRpbCB3ZSBnZXtbJiomXX10IGEgZGlmZmVyZW50IHZhbHVlIAogICAgICogb24gYm90aCBwb2ludGVycyB0aGlzIGlzIHRoZSBub2RlIHdoZXJlIHRoZSBwYXRoe1smKiZdfSBmb3Igbm9kZTEgCiAgICAgKiBhbmQgbm9kZTIgZGl2ZXJnZXMsIGFuZCBoZW5jZSwgdGhlIHByZXZpb3VzIG5vZGUgaXMgdGhlIAp7WyYqJl19ICAgICAqIGxDQSBmb3Igbm9kZTEgYW5kIG5vZGUgMi4KICAgICAqLwogICAgd2hpbGUgKHAxICZndDs9IDAgJmFtcDsmYW1wOyBwMntbJiomXX0gJmd0Oz0gMCkgewogICAgICAgIGlmIChwYXRoMS5nZXQocDEpID09IHBhdGgyLmdldChwMikpIHsKICAgICAgICAgICAgcHJldk1he1smKiZdfXRjaGluZ05vZGUgPSBwYXRoMS5nZXQocDEpOwogICAgICAgICAgICBwMS0tOwogICAgICAgICAgICBwMi0tOwogICAgICAgIH0gZWx7WyYqJl19c2UgewogICAgICAgICAgICBicmVhazsKICAgICAgICB9CiAgICB9CgogICAgU3lzdGVtLm91dC5wcmludGxuKFxcXCJPdXRwdXQ6IFxcXCJ7WyYqJl19K3ByZXZNYXRjaGluZ05vZGUpOwoKfQoKcHVibGljIHN0YXRpYyBib29sZWFuIHJvb3RUb05vZGVQYXRoKE5vZGUgbm9kZSwgQXJyYXtbJiomXX15TGlzdCZsdDtJbnRlZ2VyJmd0OyBwYXRoLCBOb2RlIG5vZGVUb0ZpbmQpIHsKICAgIGlmIChub2RlLnZhbCA9PSBub2RlVG9GaW5ke1smKiZdfS52YWwpIHsKICAgICAgICByZXR1cm4gdHJ1ZTsKICAgIH0KCiAgICBib29sZWFuIHJlcyA9IGZhbHNlOwogICAgYm9vbGVhbiBhZGR7WyYqJl19ZWRJblBhdGggPSBmYWxzZTsKICAgIGZvciAoaW50IHZhbCA6IG5vZGUuY2hpbGRyZW4pIHsKICAgICAgICAvKgogICAgICAgICAqIHtbJiomXX10aGlzIG9yIG9wZXJhdG9yIHBsYXlzIGEgdmVyeSBjcnV0aWFsIHJvbGUgaGVyZSAKICAgICAgICAgKiBhcyB3aGlsZSBiYWNrdHJhe1smKiZdfWNraW5nIGluIHBvc3RvcmRlciwgd2UgZG9udCB3YW50IAogICAgICAgICAqIHRvIGFnYWluIHZpc2l0IGV2ZXJ5IG5vZGUuIGluc3R7WyYqJl19ZWFkLCB3ZSB3YW50IHRvIGdvCiAgICAgICAgICogc3RyYWlnaHQgYmFjayB0byB0aGUgaW1tZWRpYXRlIHBhcmVudCByYXRoZXIgdHtbJiomXX1oYW4gIAogICAgICAgICAqIGV4cGxvcmluZyBpdHMgc2libGluZ3MuCiAgICAgICAgICovCiAgICAgICAgcmVzID0gcmVzIHx8IHJve1smKiZdfW90VG9Ob2RlUGF0aChub2RlTWFwLmdldCh2YWwpLCBwYXRoLCBub2RlVG9GaW5kKTsKICAgICAgICBpZiAocmVzICZhbXA7JmFtcDt7WyYqJl19ICFhZGRlZEluUGF0aCkgewogICAgICAgICAgICBwYXRoLmFkZCh2YWwpOwogICAgICAgICAgICBhZGRlZEluUGF0aCA9IHRydWU7CntbJiomXX0KICAgICAgICAvKiBhbHNvIHdlIG5lZWQgdG8ga2VlcCB0cmFjayB0aGF0IGF0IGFueSBwYXJ0aWN1bGFyIGxldmVsCiAgICAgICAge1smKiZdfSAqIHdlIHdhbnQgb25seSBvbmUgbm9kZSB0byBiZSBhZGRlZCBpbnRvIAogICAgICAgICAqIG91ciByb290IHRvIG5vZGUgcGF0aC57WyYqJl19Ki8KCiAgICAgICAgfQogICAgfQogICAgcmV0dXJuIHJlczsKfVwiO3tbJiomXX0=[[/code]]}
When you run above program, you will get below output:
18
1 2
1 3
1 4
2 5
2 6
3 7
4 8
4 9
4 10
5 11
11 12
11 13
7 14
7 15
15 16
15 17
15 18
6 13
[6, 2, 1] [13, 11, 5, 2, 1] Output: 2That’s all about Lowest Common Ancestor for any K-ary Tree
Was this post helpful?
Let us know if this post was helpful. Feedbacks are monitored on daily basis. Please do provide feedback as that\'s the only way to improve.