In this article, we will look at an interesting problem related to the Strings and [Sliding-Window Algorithm](https://java2blog.com/sliding-window-maximum-java/ “Sliding-Window Algorithm”). The problem is : "Given a String we have to Find the Maximum Number of Vowel Letters present in any Substring of the String, with the length of each Substring equal to K."
Table of Contents
Let us understand this statement with some Sample inputs:
|
1 2 3 4 5 6 7 8 |
Input: String = "java2blog" K = 3 Output: 2 Explanation: The Substrings with length K=3 for the Given String are: "jav" , "ava", "va2", "a2b", "2bl", "blo", "log". Out of which the Substring "ava" has the maximum number of vowels i.e. 2. Input: String = "looijk" K = 3 Output: 3 (Substring "ooi" has Maximum Vowel Letters). |
Now, we will discuss different approaches to solve the problem and analyze their complexities.
Approach – 1 Generate All Substrings Using substring() Method
- Basically, we will iterate throughout the length of the String and generate [all substrings](https://java2blog.com/find-all-substrings-of-string-in-java/ “all substrings”) of the given length K using the
substring()method present inStringclass ofjava.langpackage. - We Keep a Variable maxVowels which will be used to track the Maximum Vowels for a substring. So, For each substring, we count the number of Vowels in it and update the maxVowels.
- To count the number of vowels in a substring, we implement
countVowelsInSubstring(), a method which given a substring will return the count of Vowels in it.
Let us look at the code for this approach:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
public class MaxVowelsSubstring { static int maxVowelsInSubstring(String s,int k) { int n = s.length(); int maxVowels = 0; // we iterate till n-k th position of the string for(int i = 0;i < n - k ;i++) { // We generate the substring of length k using substring(). String sub_s = s.substring(i,i+k); //then count the vowels in the substring int vowels = countVowelsInSubstring(sub_s); // update maxVowels if current vowels is greater. maxVowels = Math.max(maxVowels,vowels); } return maxVowels; } static int countVowelsInSubstring(String s) { int countVowels = 0; for(int i=0; i<s.length();i++) { //get current char char ch = s.charAt(i); // check if it is a vowel and increment count. if(ch == 'a' || ch == 'e' || ch == 'i' || ch == 'o' || ch == 'u' ) countVowels++; } return countVowels; } public static void main(String args[]) { String str = "java2blog"; int k = 3; int result = maxVowelsInSubstring(str,k); System.out.println("The Maximum Vowels present in the Substring of size "+k+" is : "+result); } } |
Output:
|
1 2 3 |
The Maximum Vowels present in the Substring of size 3 is : 2 |
Time Complexity: Generating a Substring of size K using substring() method takes O(K) time and we do this for N-K characters taking total O( (N-K) * K ) time. Now, for each substring of size K, we count the vowels in it which takes total O( K * K) = O(K2) time, so the Overall [time complexity](https://java2blog.com/introduction-to-complexity-of-algorithm/ “time complexity”) will be : O( N*K -K2 + K2) = O(N * K). This is a naïve solution for this problem.
Approach – 2 Using Sliding Window Method (Linear Time Solution)
The intention behind this approach is to give a Linear Runtime Solution(O(n)) to this problem. For this, we are going to use the idea of the Sliding Window Method. We follow these steps:
- At first, we will calculate the number of vowels in the first window of size K i.e. from the index 0 to K-1 as
countVowels. We have a variablemaxVowelsthat keeps track of the maximum number of vowels in a window. - If the First Window has vowels we update the maxVowels. Then we start traversing from index K throughout the length of the String and calculate the vowels in each window. Consider the String
"java2blog"the vowels present at different windows of the string is shown below:
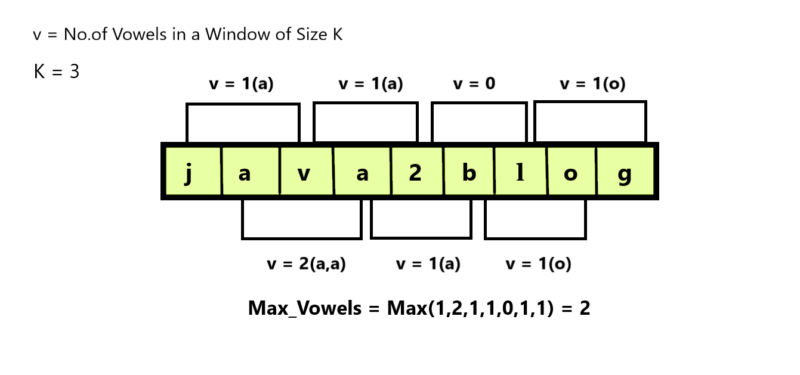
- We use the idea of prefix array, after getting the vowels in 1st window, we start from the index
K, if the character at index K is a vowel we increment thecountVowelsand if the character at the indexi - kis a Vowel we decrementcountVowelsby 1. This step ensures the window slides to the right in every iteration. - Finally, we update the
maxVowelsfor each window that we process.
Now, let us have a look at the implementation of above approach in Code:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
public class MaxVowelsSubstring { static boolean isVowel(char ch) { if(ch == 'a' || ch == 'e' || ch == 'i' || ch == 'o' || ch == 'u') return true; return false; } static int maxVowelsInSubstring(String s,int k) { int countVowels=0; //Maintains overall count of vowels // Count vowels in First Window for(int i=0;i<k;i++) { if(isVowel(s.charAt(i))) countVowels++; } int maxVowels = 0; // Update maxVowels for first window. if(maxVowels< countVowels) maxVowels = countVowels; for(int i=k;i<s.length();i++) { if(isVowel(s.charAt(i))) // check if current char is a vowel. countVowels++; if(isVowel(s.charAt(i-k))) // check if starting of previous window was a vowel countVowels--; maxVowels = Math.max(maxVowels,countVowels); // update maxVowels for each window. } return maxVowels; } public static void main(String args[]) { String str = "java2blog"; int k = 3; int result = maxVowelsInSubstring(str,k); System.out.println("The Maximum Vowels present in the Substring of size "+k+" is : "+result); } } |
Output:
|
1 2 3 |
The Maximum Vowels present in the Substring of size 3 is : 2 |
Time Complexity: Basically, We slide the window throughout the length of string, N, and traverse each character only once. For each character, we check whether it is a Vowel which is an O(1) operation. So the Time Complexity of this approach is O(N) and gives an optimal solution to the problem.
That’s all about maximum number of vowels in a substring of Given Length, you can try the code with different examples considering all edge cases.



