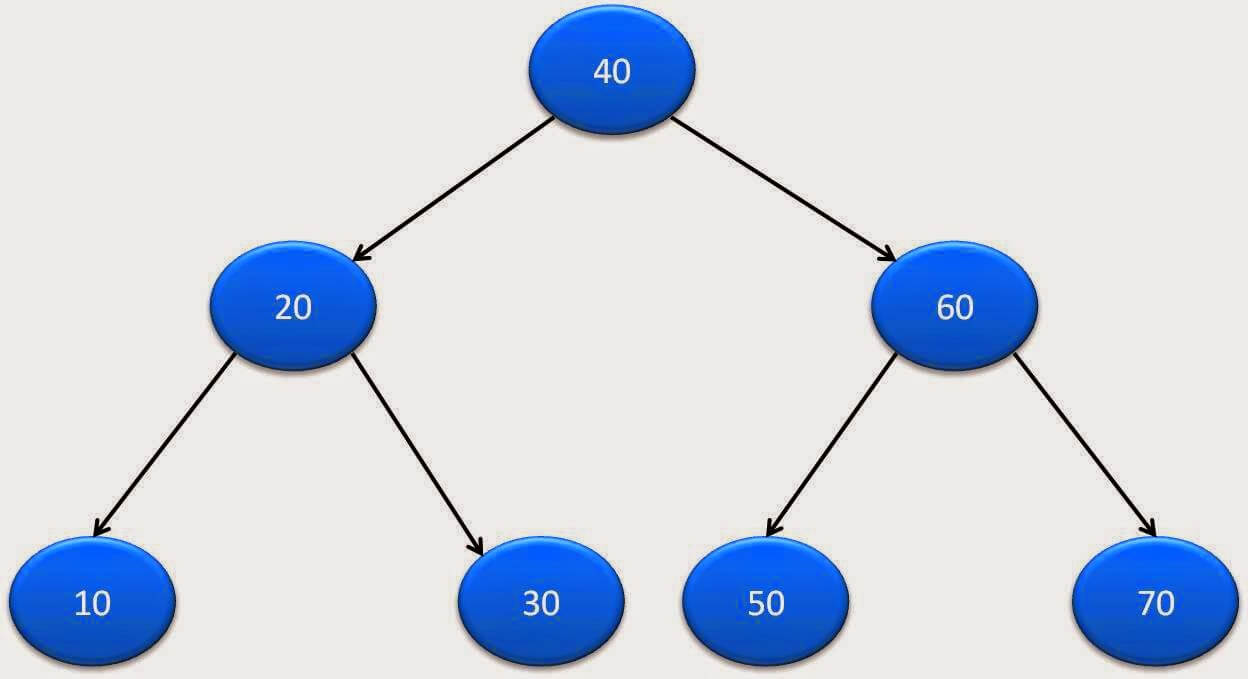
Find Maximum Element in Binary Tree in Java

• Find maximum element in left subtree.
• Find maximum element in right subtree.
• Compare maximum of above subtrees to current node.
• We will find maximum element with the above steps.

Code for recursion will be:

  // Recursive Solution
 /* To get max node in a binary tree*/
 // Recursive Solution
    /* To get the max node in a binary tree*/
    public static  int getMaximumRec(TreeNode root)
    {
        int max=Integer.MIN_VALUE;
        int value=0;
        int left,right;
        if(root != null)
        {
            value=root.data;
            left=getMaximumRec(root.left);
            right=getMaximumRec(root.right);

            if(left>right)
            {
                max=left;
            }
            else
            {
                max=right;
            }

            if(max < value)
            {
                max=value;
            }
        }

        return max;
    }

Time Complexity: O(n), where n is the number of nodes, as it visits each node exactly once.
Space Complexity: O(h), where h is the height of the tree, due to the recursion stack.

3.2 Iterative

Code for iteration will be :

        // Iterative Solution
    /* To get max node in a binary tree*/
    public static int getMaximumItr(TreeNode startNode) {

        Queue<TreeNode> queue=new LinkedList<>();
        queue.add(startNode);
        int max=Integer.MIN_VALUE;
        while(!queue.isEmpty())
        {
            TreeNode tempNode=queue.poll();
            if(max < tempNode.data)
                max=tempNode.data;
            if(tempNode.left!=null)
                queue.add(tempNode.left);
            if(tempNode.right!=null)
                queue.add(tempNode.right);
        }
        return max;
    }

Time Complexity: O(n), similar to the recursive solution.
Space Complexity: O(h), but since it’s iterative, it avoids the potential stack overflow issue.

4. Complete Java Program

Let’s say our binary tree is:

import java.util.LinkedList;
import java.util.Queue;

public class BinaryTreeGetMaxElement {
    /*
     * @Author : Arpit Mandliya
     */

    public static class TreeNode
    {
        int data;
        TreeNode left;
        TreeNode right;
        TreeNode(int data)
        {
            this.data=data;
        }
    }

    // Recursive Solution
    /* To get the max node in a binary tree*/
    public static  int getMaximumRec(TreeNode root)
    {
        int max=Integer.MIN_VALUE;
        int value=0;
        int left,right;
        if(root != null)
        {
            value=root.data;
            left=getMaximumRec(root.left);
            right=getMaximumRec(root.right);

            if(left>right)
            {
                max=left;
            }
            else
            {
                max=right;
            }

            if(max < value)
            {
                max=value;
            }
        }

        return max;
    }

    // Iterative Solution
    /* To get max node in a binary tree*/
    public static int getMaximumItr(TreeNode startNode) {

        Queue<TreeNode> queue=new LinkedList<>();
        queue.add(startNode);
        int max=Integer.MIN_VALUE;
        while(!queue.isEmpty())
        {
            TreeNode tempNode=queue.poll();
            if(max < tempNode.data)
                max=tempNode.data;
            if(tempNode.left!=null)
                queue.add(tempNode.left);
            if(tempNode.right!=null)
                queue.add(tempNode.right);
        }
        return max;
    }

    public static void main(String[] args)
    {
        // Creating a binary tree
        TreeNode rootNode=createBinaryTree();
        System.out.println("Max node using recursion :"+getMaximumRec(rootNode));
        System.out.println("Max node using iteration :"+getMaximumItr(rootNode));
    }

    public static TreeNode createBinaryTree()
    {

        TreeNode rootNode =new TreeNode(40);
        TreeNode node20=new TreeNode(20);
        TreeNode node10=new TreeNode(10);
        TreeNode node30=new TreeNode(30);
        TreeNode node60=new TreeNode(60);
        TreeNode node50=new TreeNode(50);
        TreeNode node70=new TreeNode(70);

        rootNode.left=node20;
        rootNode.right=node60;

        node20.left=node10;
        node20.right=node30;

        node60.left=node50;
        node60.right=node70;

        return rootNode;
    }
}

Run the above program, and you will get the following output:

Max node using recursion :70
Max node using iteration :70

5. Conclusion

In this article, we covered about how to find maximum element in binary tree. We have done traversal using two approaches: Iterative and Recursive. We also discussed about time and space complexity for the solutions.
Java Binary tree tutorial:

• Binary tree in java
• Binary tree preorder traversal
• Binary tree postorder traversal
• Binary tree inorder traversal
• Binary tree level order traversal
• Binary tree spiral order traversal
• Binary tree reverse level order traversal
• Binary tree boundary traversal
• Print leaf nodes of binary tree
• Count leaf nodes in binary tree
• get maximum element in binary tree
• Print all paths from root to leaf in binary tree
• Print vertical sum of binary tree in java
• Get level of node in binary tree in java
• Lowest common ancestor(LCA) in binary tree in java

Please go through java interview programs for more such programs.