If you want to practice data structure and algorithm programs, you can go through data structure and algorithm interview questions.
In this post, we will see how to search an element in sorted and rotated array.
Problem:
You are given an sorted and rotated array as below:
|
1 2 3 |
int arr[]={16,19,21,25,3,5,8,10}; |
If you note that array is sorted and rotated. You need to search an element in above array in o(log n) time complexity.
Solution:
You can search an element in above array using linear search but that will take o(n).
You can use variant of binary search algorithm to solve above problem. You can use a property that you can divide array into two sorted sub arrays ({16,19,21,25},{3,5,8,10} ), although you do not need to find pivot point(Elements start decreasing).
Algorithm:
- Compute mid i.e low+high/2.
- Check if a[mid…high] is sorted
- If number lies between the range , low=mid+1.
- If number does not lie in the range, high=mid-1.
- Check if a[low..mid] is sorted.
- If number lies between the range, high=mid-1..
- If number does not lie in the range,low=mid+1.
Lets understand this with the help of example.
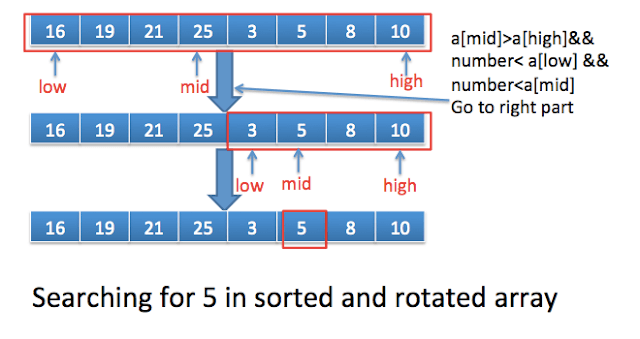
Steps involved to search 5 in above array:
- Compute mid i.e. 3 (0+7/2)
- a[mid](25) > a[high](10) && 5 < a[low](16) && 5< a[high] (25), so number (5) lies in right part, so low will become mid+1.
- a[mid] ==5, so you can return it.
Java program to search an element in a sorted and rotated array :
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
package org.arpit.java2blog; public class SearchElementSortedAndRotatedArrayMain { public static void main(String[] args) { int arr[]={16,19,21,25,3,5,8,10}; System.out.println("Index of element 5 : "+findElementRotatedSortedArray(arr,0,arr.length-1,5)); } public static int findElementRotatedSortedArray(int[] arr,int low,int high,int number) { int mid; while(low<=high) { mid=low + ((high - low) / 2);; if(arr[mid]==number) { return mid; } if(arr[mid]<=arr[high]) { // Right part is sorted if(number > arr[mid] && number <=arr[high]) { low=mid+1; } else { high=mid-1; } } else { // Left part is sorted if(arr[low]<=number && number < arr[mid]) { high=mid-1; } else { low=mid+1; } } } return -1; } } |
|
1 2 3 |
Index of element 5 : 5 |
