I will divide heap sort in multiple parts to make it more understandable.
Table of Contents
What is heap?
A heap is a tree with some special properties, so value of node should be greater than or equal to(less than or equal to in case of min heap) children of the node and tree should be complete binary tree.
Binary heaps
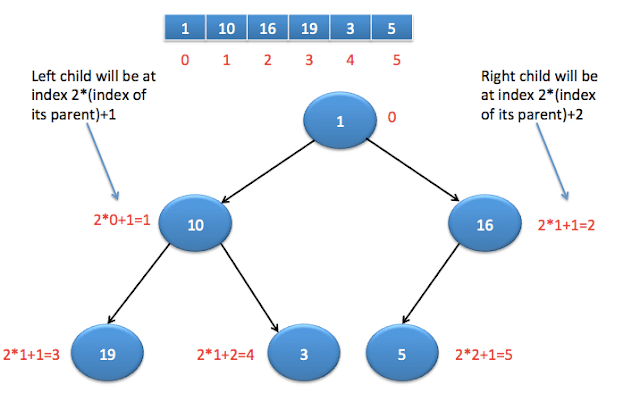
Binary heaps are those heaps which can have up to 2 children. We will use binary heaps in our next few sections.Understanding complete binary tree
Index of left child= 2*(index of its parent)+1
Index of right child= 2*(index of its parent)+2
Types of heaps
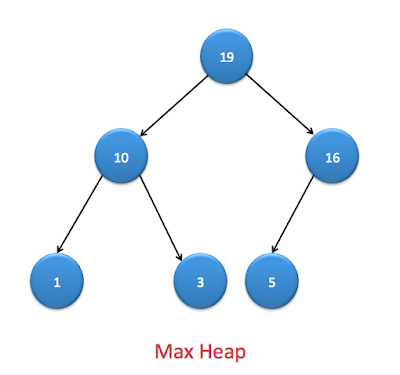
- Max heap
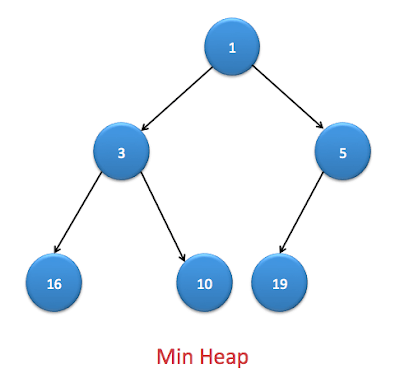
- Min heap
Max heap : It is binary heap where value of node is greater than left and right child of the node.
Min heap : It is binary heap where value of node is lesser than left and right child of the node.
Heapifying an element:
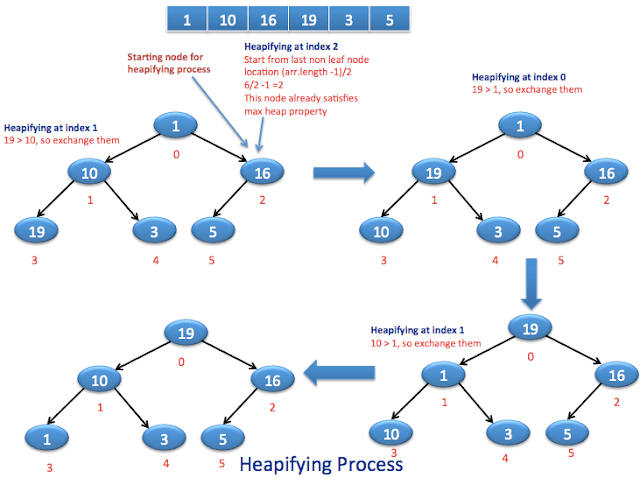
Once we create a heap , it may not satisfy heap property. In order to make it heap again, we need to adjust locations of the heap and this process is known as heapifying the elements.
In order to create a max heap, we will compare current element with its children and find the maximum, if current element is not maximum then exchange it with maximum of left or right child.
Java code for heapifying element at location i :
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
public static void heapify(int[] arr, int i, int size) { int left = 2 * i + 1; int right = 2 * i + 2; int max; if (left <= size && arr[left] > arr[i]) { max = left; } else { max = i; } if (right <= size && arr[right] > arr[max]) { max = right; } // If max is not current node, exchange it with max of left and right child if (max != i) { exchange(arr, i, max); heapify(arr, max, size); } } |
Steps for heap sort
- Represent array as complete binary tree.
- Left child will be at
2*i+1th location - Right child will be at
2*i+2th location.
- Left child will be at
- Build a heap.
- All the leaf nodes already satisfy heap property, so we don’t need to heapify them.
- Last leaf node will be present at
(n-1)thlocation, so parent of it will be at(n-1)/2th location, hence(n-1)/2will be location of last non leaf node. - Iterate over non leaf nodes and
heapifythe elements.
- After building a heap,
max elementwill be at root of the heap. We will exchange it with(n-1)thlocation, so largest element will be at proper place and remove it from the heap by reducing size of n. - When you exchange largest element, it may disturb max heap property, so you need to again
heapifyit. - Once you do above steps until no elements left in heap, you will get sorted array in the end.
Java code for heap sort
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
package org.arpit.java2blog; import java.util.*; public class HeapSortMain { public static void buildheap(int []arr) { /* * As last non leaf node will be at (arr.length-1)/2 * so we will start from this location for heapifying the elements * */ for(int i=(arr.length-1)/2; i>=0; i--){ heapify(arr,i,arr.length-1); } } public static void heapify(int[] arr, int i,int size) { int left = 2*i+1; int right = 2*i+2; int max; if(left <= size && arr[left] > arr[i]){ max=left; } else { max=i; } if(right <= size && arr[right] > arr[max]) { max=right; } // If max is not current node, exchange it with max of left and right child if(max!=i) { exchange(arr,i, max); heapify(arr, max,size); } } public static void exchange(int[] arr,int i, int j) { int t = arr[i]; arr[i] = arr[j]; arr[j] = t; } public static int[] heapSort(int[] arr) { buildheap(arr); int sizeOfHeap=arr.length-1; for(int i=sizeOfHeap; i>0; i--) { exchange(arr,0, i); sizeOfHeap=sizeOfHeap-1; heapify(arr, 0,sizeOfHeap); } return arr; } public static void main(String[] args) { int[] arr={1,10,16,19,3,5}; System.out.println("Before Heap Sort : "); System.out.println(Arrays.toString(arr)); arr=heapSort(arr); System.out.println("====================="); System.out.println("After Heap Sort : "); System.out.println(Arrays.toString(arr)); } } |
When you run above program, you will get below output:
[1, 10, 16, 19, 3, 5] =====================
After Heap Sort :
[1, 3, 5, 10, 16, 19]
Time and space complexity
Time Complexity:
Best case : O(nlogn)
Average case : O(nlogn)
Worst case : O(nlogn)
space complexity:
Since heap sort is inplace sorting algorithm, space complexity is o(1). You don’t need any extra space except swapping variable in heap sort.
What is the time and space complexity of this solution?
Hi Vivek,
Thanks for the comment. I have updated the time and space complexity in the article.