Table of Contents
If you want to practice data structure and algorithm programs, you can go through data structure and algorithm interview questions.
1. Overview
In this post, we will see how to search an element in sorted and rotated array.
2. Introduction to Problem Statement
We are given an sorted and rotated array as below:
|
1 2 3 |
int arr[]={16,19,21,25,3,5,8,10}; |
Our goal is search an element in above array in o(log n) time complexity.
Input: arr[] = {16,19,21,25,3,5,8,10}, element = 5
Output: Found at index 5.Input: arr[] = {16,19,21,25,3,5,8,10}, element = 11
Output: -1 (Not found).
3. Using Binary Search Variant
We can use variant of binary search algorithm to solve above problem. We can use a property that we can divide array into two sorted sub arrays ({16,19,21,25},{3,5,8,10} ), although you do not need to find pivot point(Elements start decreasing).
Algorithm:
- Compute mid i.e low+high/2.
- Check if a[mid…high] is sorted
- If number lies between the range, set low=mid+1.
- If number does not lie in the range, set high=mid-1.
- Check if a[low..mid] is sorted.
- If number lies between the range, set high=mid-1.
- If number does not lie in the range, set low=mid+1.
Lets understand this with the help of example.
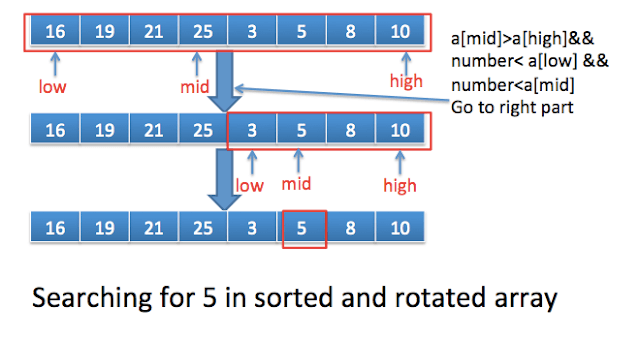
Steps involved to search 5 in above array:
- Compute mid i.e. 3 (0+7/2)
- a[mid](25) > a[high](10) && 5 < a[low](16) && 5< a[mid] (25), so number (5) lies in right part, so low will become mid+1.
- In next iteration, a[mid]==5, so we can return it.
When you run above program, you will get below output:
Time Complexity: o(logn) as binary search takes log n comparison to find an element.
Space Complexity: o(1) as there is no extra space used here.
4. Using Linear Search
We can find element in the array using linear search, but time complexity is o(n).
Steps to find element in the array using linear search:
- Iterate over the array
- In each iteration, if current element is equal to key, return the index.
- Return -1, in case we don’t find element in the array.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
class LinearSearch { // This method returns index of element x in arr[] static int linearSearch(int arr[], int x) { for (int i = 0; i < arr.length; i++) { // Return the index of the element if the element // is found if (arr[i] == x) return i; } // return -1 if the element is not found return -1; } public static void main(String[] args) { int arr[]={16, 19, 21, 25, 3, 5, 8, 10}; int x = 5; int index = linearSearch(arr, x); if (index == -1) System.out.println("Element is not found in the array"); else System.out.println("Element found at position " + index); } } |
|
1 2 3 |
Element found at position: 5 |
Time Complexity: o(n) as we iterated over array once.
Space Complexity: o(1) as there is no extra space used here.
5. Conclusion
In this article, we have coverted two ways to search element in sorted and and rotated array. Linear search takes O(n) time and not optimal while binary search takes o(logn) and is faster than linear search.