Table of Contents
If you want to practice data structure and algorithm programs, you can go through data structure and algorithm interview questions.
1. Introduction to Problem
You are given arrival and departure time of trains reaching to a particular station. You need to find minimum number of platforms required to accommodate the trains at any point of time.
For example:
|
1 2 3 4 5 |
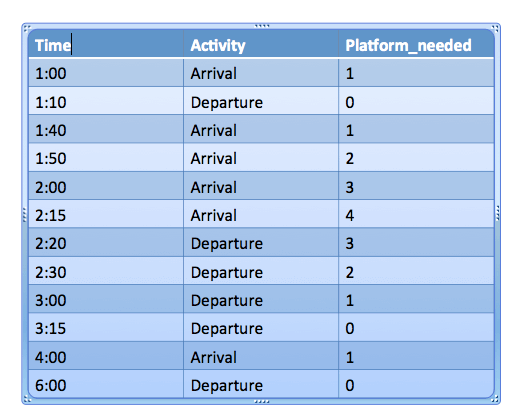
arrival[] = {1:00, 1:40, 1:50, 2:00, 2:15, 4:00} departure[] = {1:10, 3:00, 2:20, 2:30, 3:15, 6:00} No. of platforms required in above scenario = 4 |
Please note that arrival time is in chronological order.
If you notice we need to find maximum number of trains that can be on the station with the help of arrival and departure time.
2. Using Brute Force Method
You can iterate over all intervals and check how many other intervals are overlapping with it but that will require o(N^2) time complexity.
3. Using Sorting and Comparing Arrival and Departure Array
We will use logic very much similar to merge sort.
- Sort both arrival(arr) and departure(dep) arrays.
- Compare current element in arrival and departure array and pick smaller one among both.
- If element is pick up from arrival array then increment
platform_needed. - If element is pick up from departure array then decrement
platform_needed. - While performing above steps, we need track count of maximum value reached for
platform_needed. - In the end, we will return maximum value reached for platform_needed.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
package org.arpit.java2blog; import java.util.Arrays; public class TrainPlatformMain { public static void main(String args[]) { // arr[] = {1:00, 1:40, 1:50, 2:00, 2:15, 4:00} // dep[] = {1:10, 3:00, 2:20, 2:30, 3:15, 6:00} int arr[] = {100, 140, 150, 200, 215, 400}; int dep[] = {110, 300, 220, 230,315, 600}; System.out.println("Minimum platforms needed:"+findPlatformsRequiredForStation(arr,dep,6)); } static int findPlatformsRequiredForStation(int arr[], int dep[], int n) { int platform_needed = 0, maxPlatforms = 0; Arrays.sort(arr); Arrays.sort(dep); int i = 0, j = 0; // Similar to merge in merge sort while (i < n && j < n) { if (arr[i] < dep[j]) { platform_needed++; i++; if (platform_needed > maxPlatforms) maxPlatforms = platform_needed; } else { platform_needed--; j++; } } return maxPlatforms; } } |
|
1 2 3 |
Minimum platforms needed:4 |
If you are wondering why time complexity is O(NLogN), you should go through merge sort article.
4. Conclusion
In this article, we have discussed the problem of finding the minimum number of platforms required to accommodate the trains at a station. We have seen that a naive brute force approach would take O(N^2) time complexity, where N is the number of trains. We have also presented a more efficient solution that uses sorting and comparing the arrival and departure times of the trains. This solution takes O(NLogN) time complexity.


